凸函数
开始EM算法前,我们先讨论凸函数。连续函数的一阶导数就是相应的切线斜率。一阶导数大于0,则递增;一阶倒数小于0,则递减;一阶导数等于0,则不增不减。 而二阶导数可以反映图象的凹凸。二阶导数大于0,图象为凹;二阶导数小于0,图象为凸;二阶导数等于0,不凹不凸。
现设一函数f(x),在该函数定义域的凸区间内任取两点$x_1$,$x_2$, 其中$x_1<x_2$,设一点$x=q_1x_1+q_2x_2$,($q_1$,$q_2>0$且$q_1+q_2=1$),那么该点必包含于$x_1$,$x_2$之间。
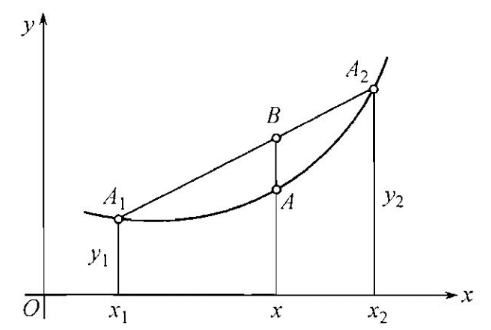
图中包含点$A_1(x_1,x_2)$、$A_2(x_2,x_2)$,$A(x,f(x))$,先构建线性函数两点式,代入$A_1(x_1,x_2)$、$A_2(x_2,x_2)$两点,再代入B点的横坐标,得到其纵坐标:
同时利用$x=q_1x_1+q_2x_2$可以得:
所以B的纵坐标是:
结合上图,显然:
且当$x_1 -> x_2$时,可以等号成立。
总结下:
在区间X上,有定义而且连续的函数$f(x)$叫做凸函数(往下凸),如果对于区间x中的任何两点$x_1$和$x_2(x_2>=x_1)$有不等式:
同理,当函数为凹函数是:
Jensen不等式
刚刚我们已经证明的凸函数的代数定义:
将其一般化,便容易推出:
将形式更加简化得:
在概率论中,如果把$p_i$看成是取值为$x_i$的离散变量x的概率分布,那么上式可以写成:
其中$E(.)$表示期望。
EM算法
EM算法是一种迭代算法,主要用来处理含有隐变量(hidden variable)的概率参数的极大似然估计,或者极大后验概率估计。EM算法的每次迭代分为两步:E步,求期望;M步,求极大。所以该算法称为期望极大算法(expectation maximization algorithm),简称EM算法。
EM算法公式推导
推导过程参照李航<统计学习方法>,加上个人理解。
当我们面对一个含有隐变量的概率模型时,我们的最终目标是要极大化观测数据$Y$关于参数$\theta$的对数似然函数,即极大化:
将所有隐变量于观测数据$Y$的所有联合概率相加,即:
注意到要极大化上式非常困难的,式中不仅有未观测数据$Z$,还包含了求和的对数,对未知变量求导后等于0的式子仍然十分复杂。 我们可以通过迭代的方式不断的逼近极大化的$L(\theta)$,假设在第i次的迭代后的$\theta$的估计值是$theta^{(i)}$,如果能够使新估计的$\theta$,让$L(\theta)$增加,即,使得$L(\theta)>L(\theta^{(i)})$,那么在一次次的迭代之后,最终会逼近$L(\theta)$的极大值。 即:
利用上面的Jensen不等式,得到其下界:
因为$P(Z|Y,\theta^{(i)})$是Z关于Y的概率分布,所以: 即上式:
令:
则:$L(\theta)≥B(\theta,\theta^{(i)})$,即函数$B(\theta,\theta^{(i)})$是$L(\theta)$的一个下界,由上面的式子可知:
因此对于任何能使$B(\theta,\theta^{(i)})$增大的$\theta$,也同时可以使$L(\theta)$增大,为了使$L(\theta)$增大,选择$\theta^{(i)}$使得$B(\theta,\theta^{(i)})$达到极大,即:
去掉不相关的常数:
EM算法的收敛性证明
由于:
两边取对数有:
等式两边同时对分布 求期望得:
等式左边与Z无关,分布求和等于1,于是:
分别取$\theta$为$\theta^{(i)}$和$\theta^{(i+1)}$并相减,有:
要使收敛性成立,只需上式右端是非负即可,又由于$Q(\theta^{(i+1)})$是$Q(\theta,\theta^{(i)})$达到极大,所以有$Q(\theta^{(i+1)},\theta^{(i)})-Q(\theta^{(i)},\theta^{(i)})≥0$, 要使右端为非负,只需$H(\theta^{(i+1)},\theta^{(i)})-H(\theta^{(i)},\theta^{(i)})≤0$,于是:
即收敛性得证。